こんにちは,M2の松田です.
私が研究で扱っているSATソルバについて,紹介したいと思います.
充足可能性問題とは
SATソルバの説明をする前に,重要な単語である充足可能性問題(SAT; Satisfiability problem)について説明します.
充足可能性問題とは,与えられた論理式を真にする変数割当てを求める問題です.
身の回りにある問題としては,パズル(数独,8クイーン)やスケジューリング問題が充足可能性問題に置き換えられます.
現在,充足可能性問題を多項式時間で解けるアルゴリズムは報告されていません.(SATはNPに属します.)
したがって,ある程度規模の大きな充足可能性問題を求めることは非常に難しいと考えられます.
そこで利用できるのが,SATソルバです.
SATソルバ
SATソルバは充足可能性問題を高速に求解するツールです.
SATソルバには多くのヒューリスティック戦略が採用されているため,ほとんどの場合高速な求解が可能です.
さらに,多くのSATソルバはOSSとなっており,だれでも利用可能となっております.
インストール
それでは,実際にSATソルバをインストールしてみましょう.
以下のコマンドで最も有名な(?)SATソルバであるMiniSatをインストールできます.
Debian系:
$ sudo apt install minisat
MacOS:
$ brew install minisat
ソースコードからビルドする場合: MiniSat(GitHub)
MiniSatについて詳しく知りたい方は,MiniSat PageやMiniSatのGitHubリポジトリをご覧ください.
使用方法
SATソルバに論理式を与えると,論理式を充足する変数割当て,あるいは論理式を充足する割当てが存在しないことを結果として返します.
SATソルバに与える論理式は連言標準形(CNF; Conjunctive normal form)で表現します.
たとえば,以下のCNFをSATソルバに与えるとします.
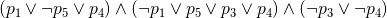
上記のCNFをSATソルバの標準入力形式(DIMACS Format)に変換すると以下のようになります.
sample.cnf:
p cnf 5 3
1 -5 4 0
-1 5 3 4 0
-3 -4 0
MiniSatのインストールが成功している場合,以下のコマンドで例題を求解できます.
$ minisat sample.cnf output(第二引数に充足結果を出力するファイルを指定)
標準出力:
============================[ Problem Statistics ]=============================
| |
| Number of variables: 5 |
| Number of clauses: 2 |
| Parse time: 0.00 s |
| Eliminated clauses: 0.00 Mb |
| Simplification time: 0.00 s |
| |
============================[ Search Statistics ]==============================
| Conflicts | ORIGINAL | LEARNT | Progress |
| | Vars Clauses Literals | Limit Clauses Lit/Cl | |
===============================================================================
===============================================================================
restarts : 1
conflicts : 0 (0 /sec)
decisions : 1 (0.00 % random) (617 /sec)
propagations : 3 (1851 /sec)
conflict literals : 0 (-nan % deleted)
Memory used : 12.00 MB
CPU time : 0.001621 s
SATISFIABLE
output:
SAT
1 -2 3 -4 5 0
この出力結果から,与えられた論理式はSAT(充足可能)であり,与えられた論理式を真にする変数割当ての一つは1=真,2=偽,3=真,4=偽,5=真のときであることがわかります.
Ravensat
私たちが開発しているSATソルバのインタフェース,Ravensatを紹介します.
SATソルバは非常に優れた求解機能を提供するAPIであり,プログラマが直接DIMACS Formatを記述することは実際ほとんどありません.
なぜなら,実用的な充足可能性問題は,通常数千から数百万の変数が定義され,これをプログラマが直接DIMACS Formatで記述するとなると以下のような問題が発生します.
- ファイルの行数は少なくとも数千行に及ぶため,記述に多大な労力がかかる.
- 変数に対して自由な命名ができないため,記述性および可読性が非常に低い.
Ravensatは上記の問題を解決するためのRubyのgemです.
Ravensatには以下のような特徴があります.
- 論理演算子(&,|,~)による論理式の記述
- 呼び出すSATソルバを指定可能
例に挙げたCNFをRavensatで記述し,MiniSatで求解するプログラム例を以下に示します.
p1, p2, p3, p4, p5 = Array.new(5){Ravensat::VarNode.new}
cnf = (p1 | ~p5 | ~p4) & (~p1 | p5 | p3 | p4) & (~p3 | ~p4)
solver = Ravensat::Solver.new('minisat')
solver.solve cnf #=> true (satisfiable)
p1.value #=> true
p3.value #=> true
p4.value #=> false
p5.value #=> false
まとめ
この記事では,充足可能性問題とSATソルバについて簡単に説明し,私たちが開発しているRavensatについても紹介しました.
SATソルバは実用的にも理論的にも面白い側面を持っています.
この機会にSATソルバに触れてみてはいかがでしょうか.
参考リンク: